这两天因为需要看了两篇 Dijkstra 的论文,将思想整理出来以供学习。
Dijkstra 算法
Dijkstra 算法的具体细节不再赘述,本质上是一种贪心算法,通过不断添加距离源点最短的点并刷新距离来求解。
稀疏图的压缩
Virtual Node
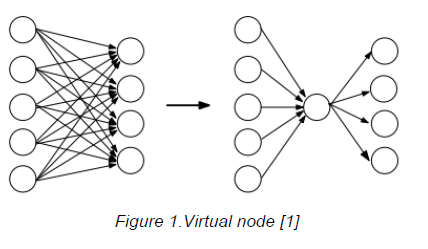
如图,通过添加点减少边的数量(子图必须是二部图)
Superedges
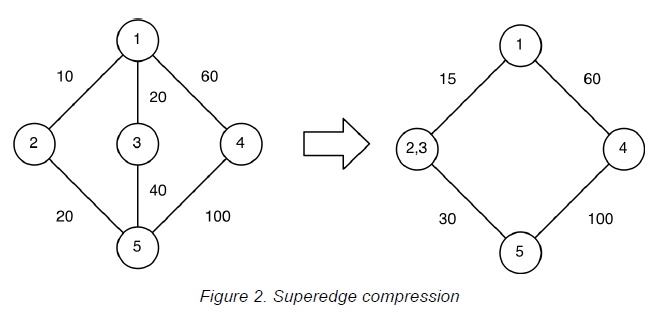
如图,合并相似点(邻接点相同、距离均相近)
动态 Dijkstra 压缩
先将所有点按度数排序(压进优先队列),每次弹出一个顶点,把它的 Dijkstra 最短路的所有路径加入新图G’中。
当G’的压缩率(G’的边数/G的边数)达到某一要求值时结束循环。
讲道理,看到这里的时候我是崩溃的。这压缩能用?
边数:
随机两点间最短距离: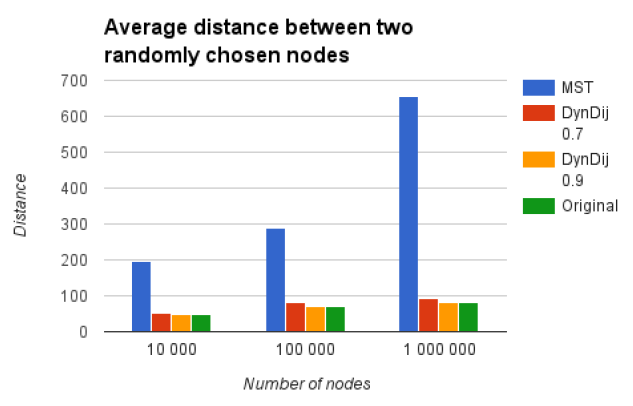
答案准确度(随机两点间最短路和原图的比):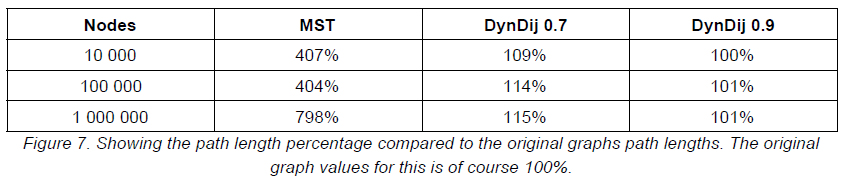
和原图的 Dijkstra 运行时间比: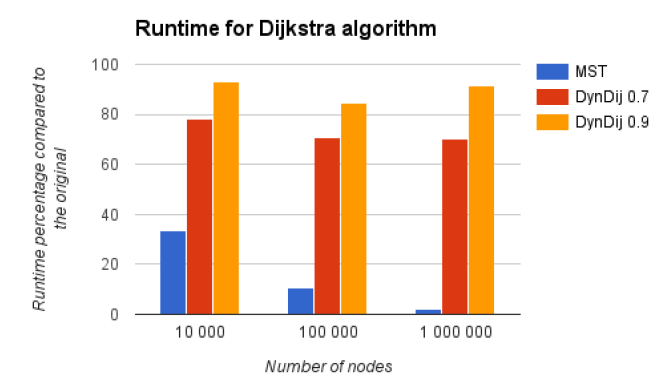

感觉作用不大啊。。
结论
试图压缩稀疏图的想法并不靠谱。压缩率在0.9的时候还能接受。然而做一次压缩所需要的时间耗费太过巨大,所以并不推荐使用图压缩。