斐波那契堆
斐波那契堆是一种相对松散的堆结构。它的存储结构并不是一棵树,而是一个森林,并且每棵树都是一个符合堆结构的多叉树。
它的特点是只在删除掉顶点以后整理堆的结构。并且通过做标记的形式保持堆的平衡。
具体操作
Insert
直接插入对应结点,松散排列。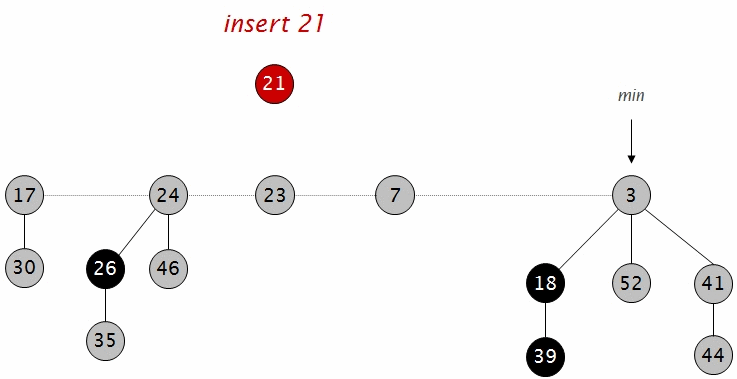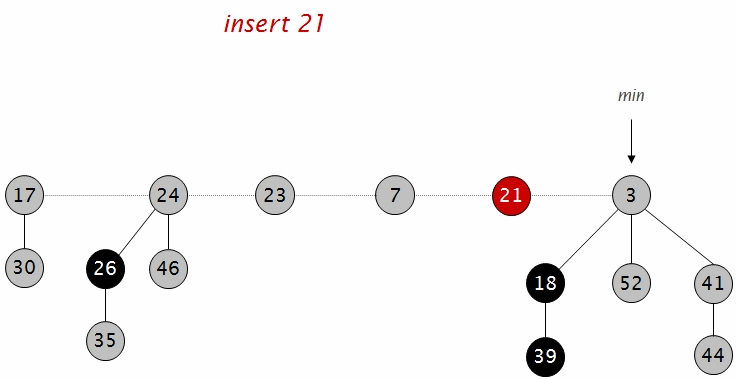
DeleteMin
删除顶点后先直接将所有子节点作为一棵树直接放进堆,然后进行整理。
整理的方式是,将rank(即根节点的孩子数)相同的树合并为一棵树。
//别问我为什么没做成 gif ,因为没有 PS ,而且懒。
去掉顶点并直接将子节点作为独立的树: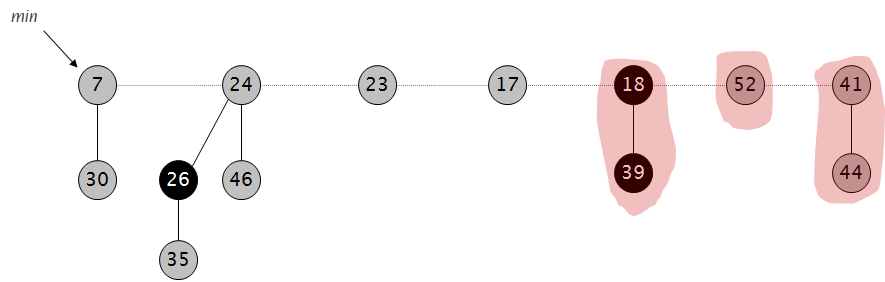
开始合并操作: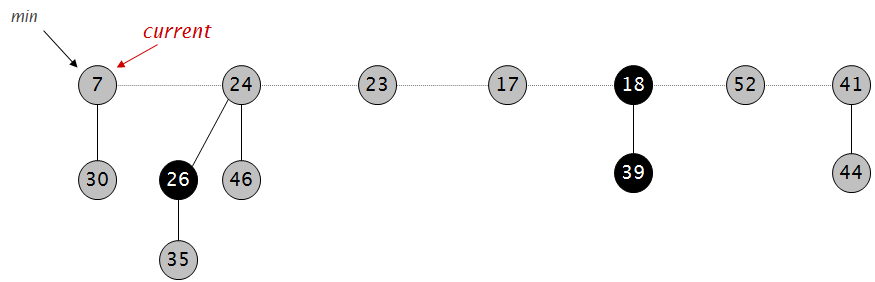
将树的根节点按照rank依次放进一个指针数组: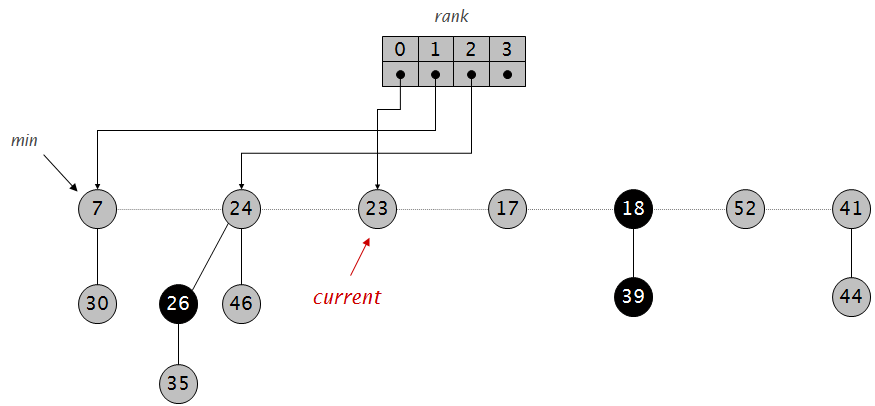
发现已经有相同rank的根节点则进行合并: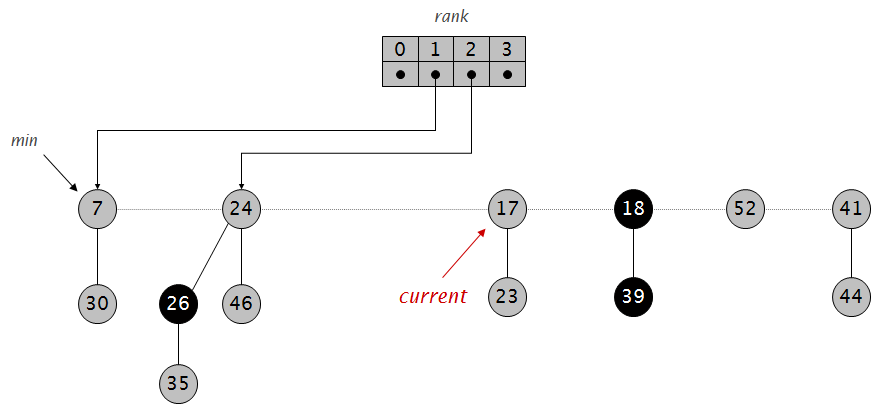
不断合并直到rank唯一: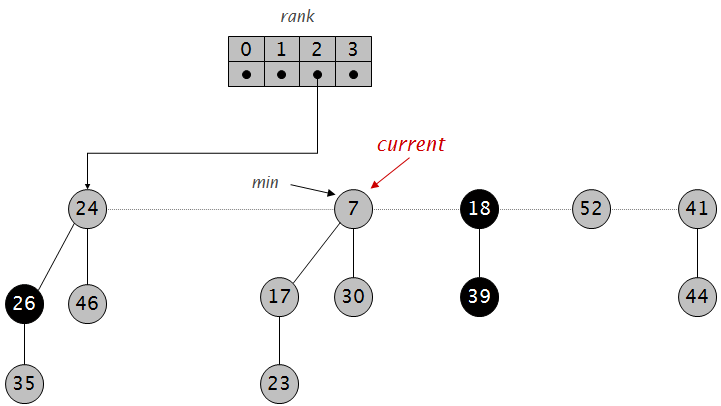
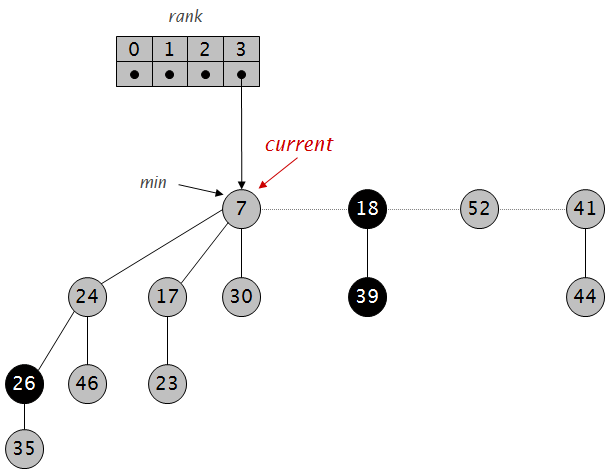
继续: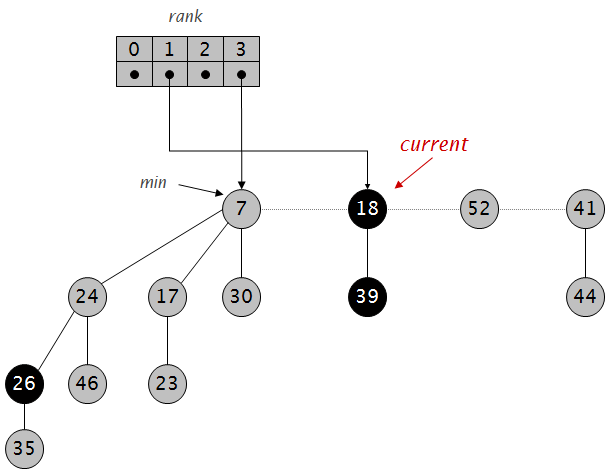
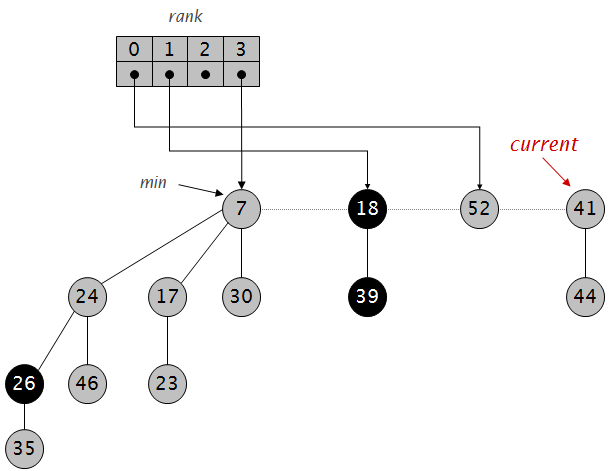
合并: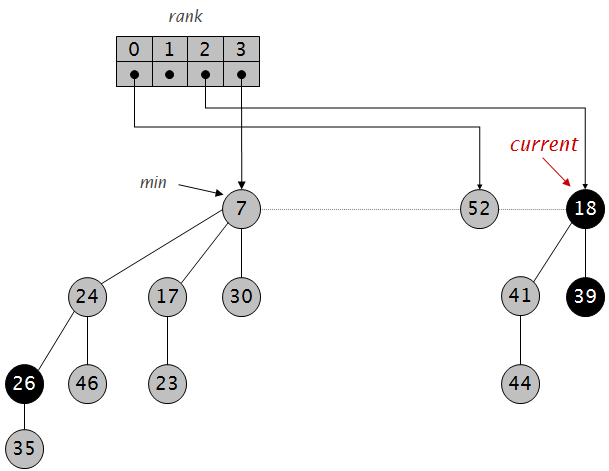
到这里,整个堆的根节点都放进数组,整理完成。
DecreaseKey
此过程需要用到之前定义的 mark 属性,它表示这一结点是否已经被删除过子节点。通过这一标记来尽量保证树的平衡,避免出现“链”的结构。
具体操作如下:
首先减小某一顶点的值,然后观察其是否是小于父节点:
若无父节点,则看是否要更新 min 指针;
若依然大于父节点,则不做修改;
若小于父节点,则剪断改分支,并尝试对父节点做标记;
若父节点已经有标记,则剪断父节点并递归对其父节点做标记,直到可以做标记或已经是根节点为止。
将46减小为29: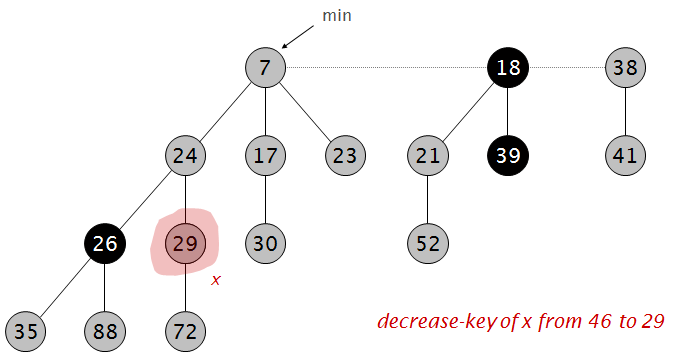
小于父节点,无需修改
将29减小为15: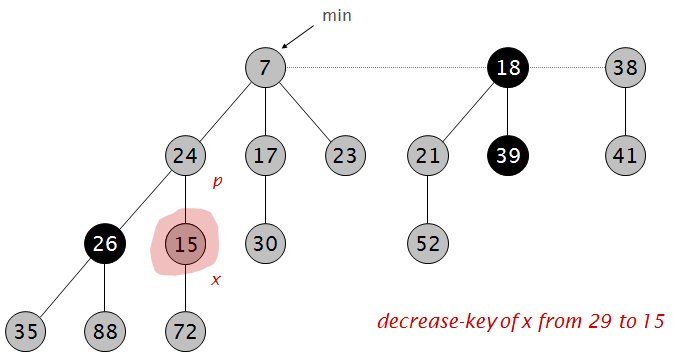
小于父节点,剪断,并做标记: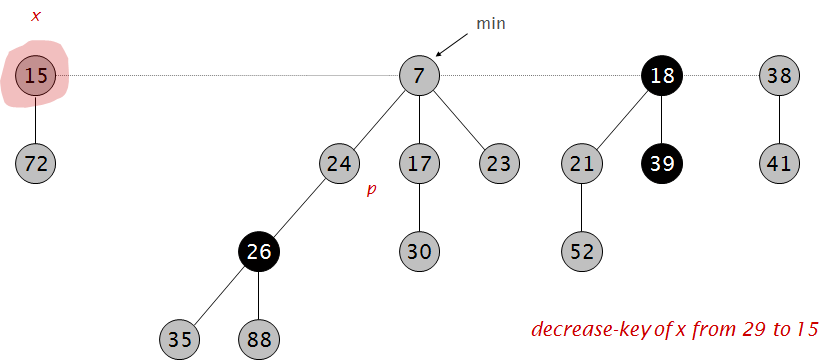
24被标记: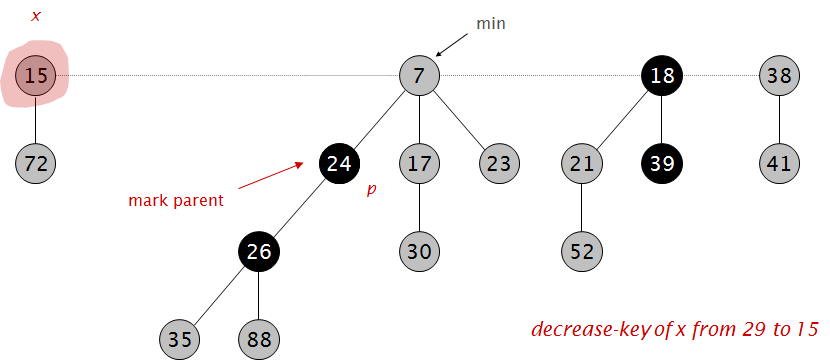
将35减小为5: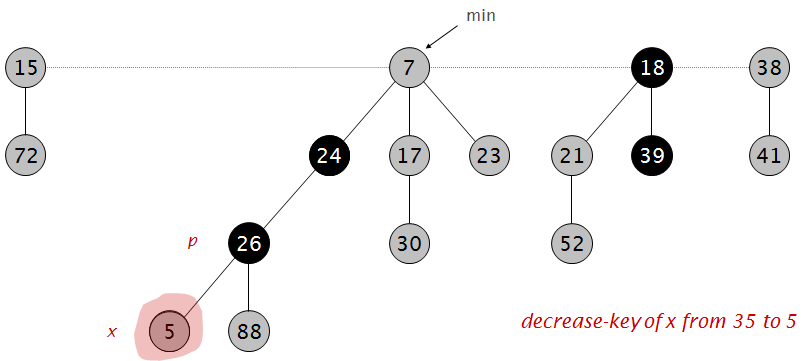
小于父节点,剪断,并做标记: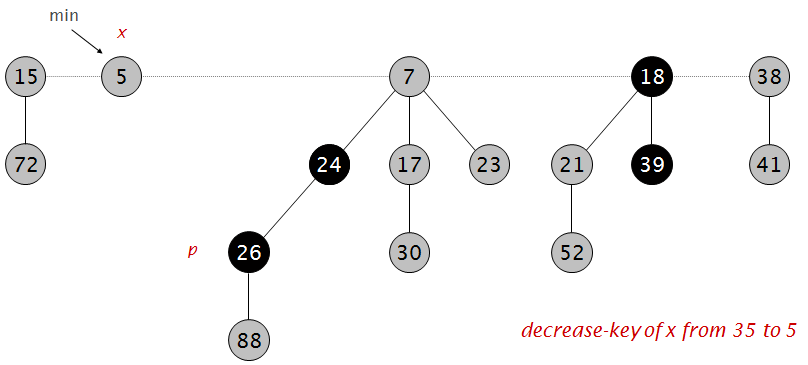
父节点已经被标记一次了,所以剪断父节点,并对其父节点做标记: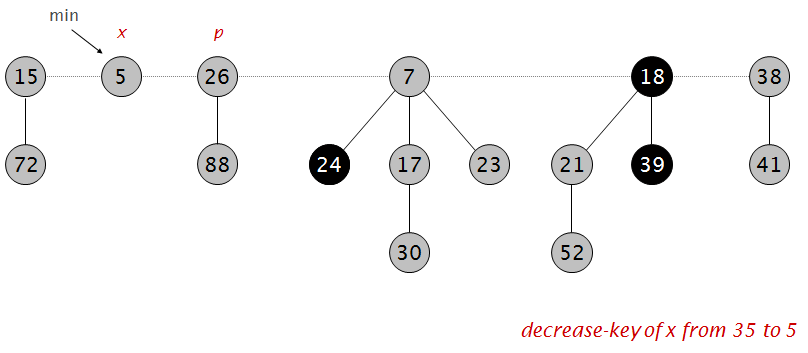
发现其父节点也已经被标记了,所以再次剪断父节点并对其父节点做标记: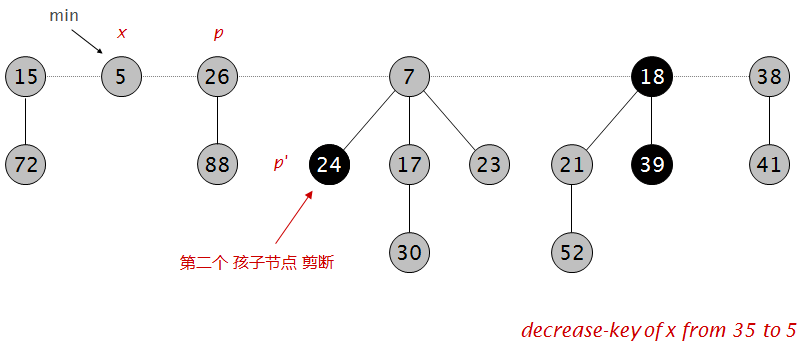
由于父节点是根节点,所以不再做标记: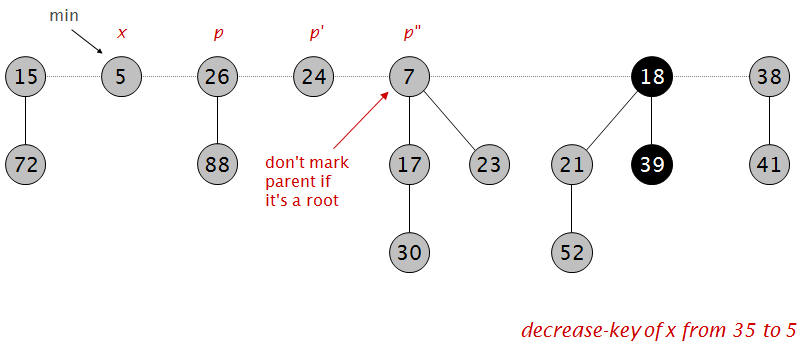
时间复杂度分析
| 符号 | 含义 |
|---|---|
| n | 节点数 |
| rank(x) | 结点 x 的孩子数 |
| rank(H) | 堆 H 的最大 rank |
| trees(H) | 堆 H 中树的数量 |
| marks(H) | 堆 H 中已标记的点数 |
定义一个势函数: Φ(H) = trees(H) + 2 marks(H)
Insert:
- 时间复杂度: O(1)
- 势函数变化: + 1
- 均摊时间复杂度: O(1)
Delete Min:
O(rank(H)) + O(trees(H))
- O(rank(H))将最小值的孩子合并到根节点列表中
- O(rank(H)) + O(trees(H)) 更新最小值
- O(rank(H)) + O(trees(H)) 巩固森林
势函数变化:O(rank(H)) - trees(H)
- trees(H’) ≤ rank(H) + 1 因为没有两个树有相同的rank
- △Φ(H) ≤ rank(H) + 1 - trees(H)
均摊时间复杂度: O(rank(H))
Decrease Key:
O(c) (c 表示剪断次数)
- O(1) 改变权值
- O(1) 剪断并放到根节点列表
势函数变化:O(1) - c
- trees(H’) = trees(H) + c
- marks(H’) ≤ marks(H) - c + 2
- △Φ ≤ c + 2 (-c + 2) = 4 - c
均摊时间复杂度: O(1)
可以证明,rank(H) ≤ log Φ (|V|)(其中Φ表示(1 + √5) / 2 ≈ 1.618),由于证明过程有点复杂这里不再说明。
所以最终复杂度为O( ( 1 + log Φ (|V|) )|V| + |E| )