旅行商问题(traveling-salesman problem)
问题描述
通常我们讨论的都是对称旅行商问题(SYMMETRIC traveling-salesman problem),即距离矩阵保持对称(A 到 B 与 B 到 A 距离相等)。
严格意义上的旅行商问题的要求是:遍历所有点,保证每个点刚好访问一次,求最短的遍历路径。
基本思路
解决这种问题的算法分为两种:精确算法(Exact algorithms)和启发式方法(heuristic methods)。
精确算法的复杂度过高(n的指数级),短时间可解决的问题约在60个点(1971)。
一般采用启发式方法去解决能得到一个相对满意的结果。
解决这个问题的灵感来自于另一个问题:图分割问题。
问题描述很简单:将图分为两个点的个数相同的部分,并满足两个部分间的距离最短。
我们可以将这两个问题抽象成同一种问题:
从集合 S 中寻找满足限制条件 C 并能使目标函数 f 最小化的子集 T 。
接下来,我们就可以将启发式算法的思路总结出来:
- 找到一个可行解,即一个满足条件 C 的子集 T
- 尝试在 T 上做一些改变,寻找比 T 更优(能使得 f 更小)的子集 T’
- 如果找到子集 T’ 更优(使得 f(T’) < f(T) ),用 T’ 替换 T 并重复上一
- 如果找不到,T 就是局部最优解。再次重复第一步直到时间到某一上限或答案已经足够满意。
在 TSP 问题中,这个问题的具体化就是:
- 从所有边构成的集合 S 中找出一个可行回路 T
- 每次从 T 中找出 k 条边,从 S-T 中找出另外的 k 条边,保证这 k 条边交换后能形成回路且费用更小
- 如果找到则进行交换
- 如果找不到,则 T 就是局部最优解。再次重复直到时间到达某一上限或答案足够满意
启发式算法的核心
这种算法好坏主要看两点:
- 第一步中找到的初始解的好坏
- 第二步中的替换算法的好坏
KL算法重点关注第二个点。
第二步中有一个难题,是 k 的值具体应该取多少?
如果遍历 k 那无疑是一件很恐怖的事,所以我们尝试用一些方法:
- 生成随机初始解 T
- 令 i = 1
- 选择第 i 步的“最不合适”对:xi 和 yi,使得 {x1, x2, …… , xi} 和 {y1, y2, …… , yi} 交换后缩短的距离值最大(具体原则在下面给出)
- 如果找不到不合适对,则进入下一步,否则重复本步骤
- 如果一个更优解已经找到,则将 x 和 y 两个集合交换,得到新的 T,重复上一步骤;若找不到更优解,则进入下一步
- 如果需要的话重复第一步
那我们采用怎样的方法去找“最不合适”对呢?
首先,我们要保证每次交换后都能得到一个可行的交换,所以我们保证 x1、y1、x2、y2 …… 依次首尾相连(且 yn 最后一个节点为 x1 的第一个节点),如下图所示: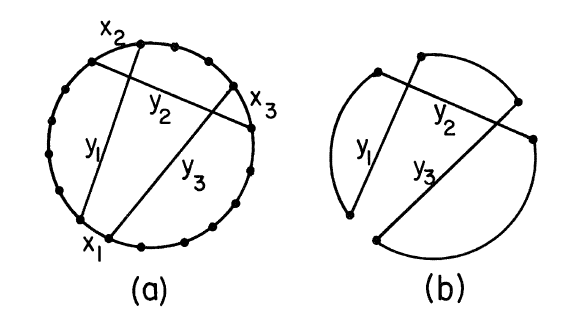
其次,假设 gi 表示 xi 与 yi 交换后减少的代价,那么我们不必在某一个 gi 为负数时立刻停止,我们只在 g1+g2+……+gi ≤ 0 时认为找不到“不合适”对。
当然,我们要保证不重新选取被去掉的边。
Kernighan-Lin 算法
具体描述
- Step 1: 生成随机回路 T
- Step 2: 令 G* = 0,任选一个点 t1 作为起始点,从 t1 出发选取回路 T 中的一条边 x1 ,假设另一端为 t2,令 i = 1
- Step 3: 从 t2 出发,选取任一不在 T 中的边 y1,假设另一端为 t3,满足 g1 > 0 。若不存在这样的 y1,则跳至 Step 6 (d)
- Step 4: 令 i = i + 1,选择 xi (T 中以 t(2i-1) 为出发点的路径)和 yi,具体说明如下:
- (a) 若 xi 连接的是 t(2i) 和 t1 ,则完成一次查找
- (b) yi 应当从 t(2i) 出发;若没有可行边,则跳转至 Step 5(显然,我们优先考虑最近的点)
- (c) x 和 y 不能有交集
- (d) G > 0
- (e) yi 的选择应保证 t(2i+1) 在 T 中有其他邻接点
- (f) 在选定 yi 前,我们观察是否连接 t(2i) 和 t1 比选择的 yi 是更好的选择(费用减少更多)。令 yi* 表示边 ( t(2i), t1 ),gi* = |xi| - |yi*| 。若 G(i-1) + gi* > G* 则更新 G* 的值为 G(i-1) + gi* 并记 i 为 k。
- Step 5: 当找不到 xi 和 yi 满足 4(c)-(e) 或 Gi ≤ G* 时,结束上一循环。若 G* > 0,更新 T’ ,且 f(T’) = f(T) - G*。以 T’ 为初始回路重复从 Step 2 开始的这一过程。
- Step 6: 如果 G* = 0,按下列方式处理:
- (a) 重复 Step 4 和 5,按升序选择满足 g1 + g2 > 0 的 y2 ,跳回 Step 2
- (b) 如果 Step 4 (b) 中所有 y2 的选项都使得 G 为负,则返回 Step 4 (a) 尝试选择另一个 x2
- (c) 如果仍然无法得到解,跳至 Step 3,按升序找新的 y1
- (d) 如果找不到合适的 y1,跳至 Step 2,尝试另一条 x1
- (e) 如果仍然失败,跳回 Step 2,重新选择 t1
生成的最终路径:
一些优化
避免校验时间(Avoiding Checkout Time)
如果回路 T 无法再次被改进,则 T 是一个局部最优解。当下次再次得到回路 T 时,避免再次检验。
可节约 30-50% 的运行时间。
预测(Lookahead)
为避免出现选择的 yi 使得 x(i+1) 太小最终导致无用的搜索,在选择 yi 时选择使得 |x(i+1)|-|yi| 最大的 yi。
减少重复搜索(Reduction)
因为很多时候,大部分重要的优化都是相同的,所以我们在找出至少两个局部最优解后,求这些最优解的交集,并以这些边作为初始回路的一部分。
数据测试发现,两个普通的局部最优解有 85% 是相似的,甚至 7-8 个最优解也有 60-80% 是相似的。
缺陷
无法进行不连续交换。
e.g.: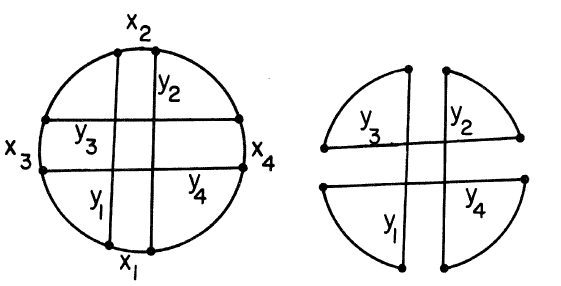
初始随机解的生成优化
根据初始随机解的生成方式的不同,衍生出不同的方法,其中包括:
- 最近插入法(nearest insertion,NI)
- 凸包法(connex hull insertion,CHI)
- 最远插入法(farthest insertion,FI)
- 最邻近法(nearest neighbor algorithm,NN)
- 节约算法(clark wright algorithm,CW)
- 贪婪算法(greedy algorithm,GA)
- 最小双生树法(double spanning tree,DST)
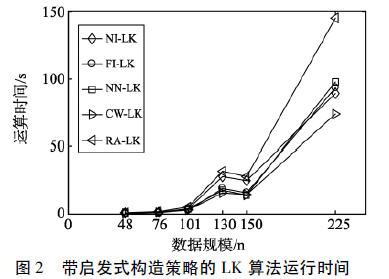
部分算法性能如下: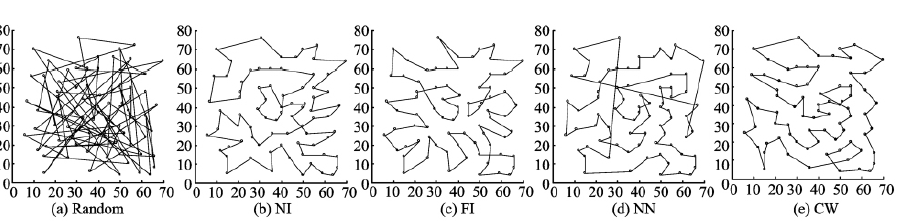
论文来自
An Effective Heuristic Algorithm for the Traveling-Salesman Problem
—— S. Lin and B. W. Kernighan
Lin-Kernighan 算法初始解的启发式构造策略
—— 曾华,崔文,付连宁,吴耀华